LeetCode 每日一题 2022-10

2022/10/12 817.链表组件

当需要多次判断值是否位于数组中时，可以采用哈希集合保存数组中的值来降低时间复杂度

// 初始化
unordered_set<int> hash;
for(int num : numList)
    hash.emplace(num);
// 查询
int num = 0;
if(hash.count(num))
    cout << "Find!" << endl;

2022/10/13 769.最多能完成排序的块

class Solution {
public:
    int maxChunksToSorted(vector<int>& arr) {
        int maxNum = -1;
        int ans = 0;
        int n = arr.size();
        for(int i = 0; i < n; i++) {
            maxNum = max(maxNum, arr[i]);
            if(maxNum == i) 
                ans++;
        }
        return ans++;
    }
};

2022/10/14 940.不同的子序列 II

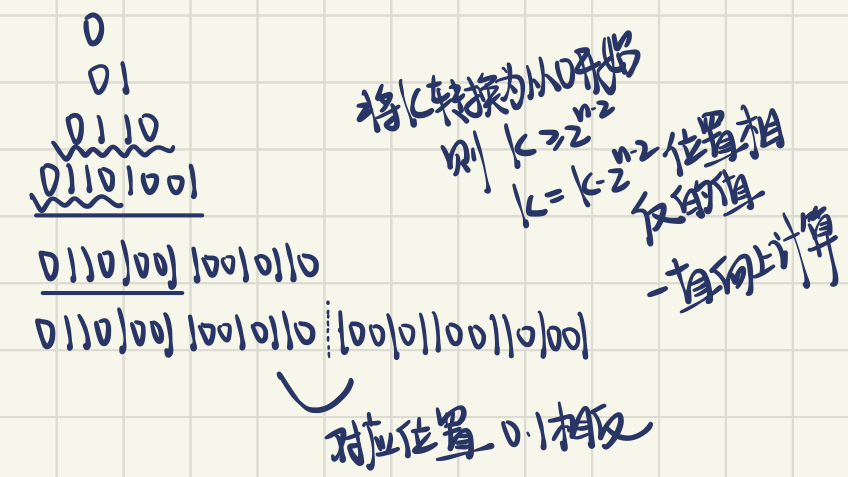
2022/10/15 1441. 用栈操作构建数组

2022/10/16 886.可能的二分法

一道判定二分图的模板题

可以用染色法或扩展域并查集解决

2022/10/17 904. 水果成篮

双指针

注意使用哈希表存储这个窗口内的数以及出现的次数更优

2022/10/18 902. 最大为 N 的数字组合

数位 DP 模板题

视频讲解

2022/10/19 1700. 无法吃午餐的学生数量

简单模拟

2022/10/20 779. 第K个语法符号

找规律

2022/10/22 1235. 规划兼职工作

动态规划

const int N = 500010;

class Solution {
public:
    int curMax[N];

    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = profit.size();
        vector<int> idList;
        for(int i = 0; i < n; i++)
            idList.emplace_back(i);

        // 按照结束时间升序排序
        sort(idList.begin(), idList.end(), [&](int i, int j) { return endTime[i] < endTime[j]; });

        curMax[0] = profit[idList[0]];
        for(int i = 1; i < n; i++) {
            int curId = idList[i];
            curMax[i] = max(profit[curId], curMax[i - 1]);
            for(int j = i - 1; j >= 0; j--) {
                int preId = idList[j];
                if(startTime[curId] >= endTime[preId]) {
                    curMax[i] = max(curMax[i], curMax[j] + profit[curId]);
                    break;
                }
            }
        }

        return curMax[n - 1];
    }
};

2022/10/23 1768. 交替合并字符串

2022/10/24 915. 分割数组

2022/10/26 862. 和至少为 K 的最短子数组

双指针超时><

涉及到 子数组和 的问题，可能与前缀和有关

前缀和

可以用 两个前缀和的差表示子数组的和

单调队列

两张图秒懂单调队列 - 和至少为 K 的最短子数组

class Solution {
public:
    int shortestSubarray(vector<int> &nums, int k) {
        int n = nums.size(), ans = n + 1;
        long s[n + 1];
        s[0] = 0L;
        for (int i = 0; i < n; ++i)
            s[i + 1] = s[i] + nums[i]; // 计算前缀和
        deque<int> q;
        for (int i = 0; i <= n; ++i) {
            long cur_s = s[i];
            while (!q.empty() && cur_s - s[q.front()] >= k) {
                ans = min(ans, i - q.front());
                q.pop_front(); // 优化一
            }
            while (!q.empty() && s[q.back()] >= cur_s)
                q.pop_back(); // 优化二
            q.push_back(i);
        }
        return ans > n ? -1 : ans;
    }
};